Review on Dynamic Analyses of Structures Under Multi-support Excitation

Article Bill of fare

/ajax/scifeed/subscribe

Open up Access Article

Influence of Multiple-Support Excitation on Seismic Response of Reinforced Concrete Curvation Bridges

Department of Engineering Mechanics, Faculty of Civil Engineering, University of Zagreb, 10000 Zagreb, Croatia

^*

Author to whom correspondence should be addressed.

Received: 1 November 2019 / Revised: half dozen December 2019 / Accustomed: sixteen December 2019 / Published: 18 December 2019

Abstract

Although post-earthquake observations identified spatial variation of ground motion (i.e., multiple-support excitation) as a frequent crusade of the unfavorable response of long-span bridges, this miracle is often not taken into business relationship in seismic design to simplify the calculation procedure. This study investigates the influence of multiple-back up excitation accounting for coherency loss and wave-passage effects on the seismic response of reinforced concrete deck arch bridges of long spans founded on rock sites. Parametric numerical study was conducted using the time-history method, the response spectrum method, and a simplified procedure according to the European seismic standards. Results showed that multiple-back up excitation had a detrimental influence on response of almost all analyzed bridges regardless of considered arch span. Both considered spatial variation effects, acting separately or simultaneously, proved to be very important, with their relative significance depending on the response values and arch locations analyzed and seismic records used. Therefore, it is suggested that all spatially variable basis-motion effects are taken into account in seismic analysis of similar bridges.

1. Introduction

Comeback of seismic pattern methods always follows new observations and analyses of damage and collapse due to major earthquakes. Conducted studies identified spatial variation of ground motion as a frequent crusade of unfavorable response of long-bridge bridges, e.g., [1,two], but this phenomenon is usually not taken into business relationship in seismic design to simplify the adding procedure. Since length and spans of larger bridges are comparable to the seismic wavelength, it is obvious that all span supports cannot be excited simultaneously. Additional differences in the seismic input to different supports ascend from changes in the frequency content and aamplitude of the seismic waves propagating from the base rock to the basis surface. Simple examples of multiple-back up excitations include the unseating of the superstructure due to differential displacements of its supports [2,3,4].

The pioneering studies of the phenomenon of basis motion spatial variation occurred in the 1960s [5], while meaning improvements in the understanding of the phenomenon may be attributed to data recorded in strong-motility arrays such as SMART-1 (Potent Motility Assortment in Taiwan—Phase 1) [half dozen], El Centro Differential Assortment, Thessaloniki in Greece, Pinyon Apartment in the Usa, amidst others [7,8]. The main causes of spatial variability in basis motions are attributed to coherency loss (loss of coherency of seismic waves due to reflections and refractions of waves in the heterogeneous medium of the ground and due to superposition of waves arriving from a seismic source), wave-passage effect (time delay in arrival of seismic waves to dissimilar supports of the construction), attenuation furnishings (disuse of amplitudes and energy of seismic wave propagating through the ground) and local site weather (different geological atmospheric condition at different supports influence frequency content and amplitudes of seismic waves) [9], schematically depicted in Figure 1. The interested reader may refer to [vii,10,eleven] for a comprehensive overview of the subject.

In general, random vibration methods, response spectrum methods and deterministic methods are used in the study of the multiple-support excitation outcome in engineering science applications. Although, numerous studies in which response of bridges to multiple-support excitation was analyzed using different methods may be plant in literature (e.g., [2,13,14,15,16,17,18,19,twenty,21,22]), very petty inquiry has been devoted to arch bridges. Some detailed studies dealt with arch structures in general (due east.one thousand., [23,24,25]), while studies of curvation bridges generally considered steel bridges [26,27,28]. The virtually of import conclusions from some of those studies will be summarized beneath. The results of the stochastic response of incompressible round arches to multiple-support excitation presented in [23] showed that neglecting multiple-support excitation effect can underestimate, merely also overestimate the response, depending on the properties of the arches, response quantities and the seismic excitation. The author concluded that wave-passage consequence was more detrimental than the loss of coherence. However, Harichandran et al. [26] studied the responses of two-deck steel arch bridges of big span and showed that the coherency loss is also very of import for response in addition to wave-passage effect. Authors concluded that compatible excitation is in general unacceptable for considered bridges. In the research [28] in which deck steel curvation bridges were analyzed, information technology was concluded that the response to the multiple-back up excitation was less detrimental than to the uniform one in the vertical and transverse directions, whereas in the longitudinal direction the multiple-support excitation significantly affects the response and should non be neglected.

Very express investigations of concrete arch bridges found in literature are those in [29,30,31,32,33]. The seismic response of an existing reinforced concrete arch span of 150 m bridge to uniform and multiple-support excitation was investigated in [29]. The authors concluded that the multiple-support excitation significantly increases the longitudinal force in the arch, even exceeding its load-begetting capacity. The like conclusion was reached past authors of [30] in which the response of several smaller-span reinforced physical curvation bridges was investigated and in [33] where authors considered only the wave-passage outcome on the response of a reinforced physical arch bridge of long span. Information technology may exist observed that no systematic study of the response of reinforced concrete arch bridges of large spans to multiple-support excitation may be found in literature.

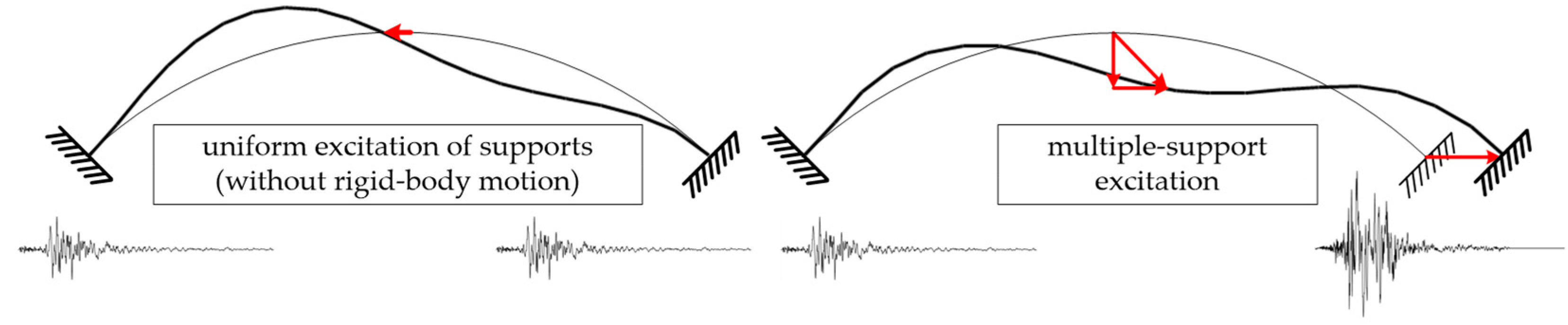
It is common cognition that the response to multiple-back up excitation differs from uniformly excited response. Due to relative displacements of the supports, a quasi-static component of the response is induced, while dynamic component of the response likewise changes considering different eigen-modes are excited to modes excited past uniform excitation. For example, in symmetrical arch bridges, uniform excitation in the longitudinal management of the bridge excites only the antisymmetric vibration modes, while in the case of multiple-support excitation, both symmetric and antisymmetric modes are activated (Figure 2), including the higher modes, which should not be neglected in the analysis. Information technology is interesting to mention studies presented in [19,34], despite the fact that a cable-stayed bridge (not an arch 1) was studied. On the basis of monitoring a real structure (free-field and on-structure recordings) it was revealed that the asynchronous excitation of a span excited college modes of vibration while suppressing the oscillation in its fundamental frequency.

To summarize, in the research community there is nonetheless no consensus whether the multiple-support excitation phenomenon is favorable or detrimental for seismic response of structures, considering it depends on many parameters, including the excitation features, soil characteristics and dynamic characteristics of excited structure. Therefore, the objective of this newspaper is to report its effect on seismic response of long-bridge reinforced concrete deck curvation bridges, the structural organisation which has not withal been investigated in detail regarding this effect. This report contributes to meliorate understanding of seismic behavior of these structures and information technology aims to requite guidelines whether the multiple-support excitation should exist considered for seismic analysis of bridges of like structural systems and spans. Analyses were conducted using state-of-the art methodologies and tools on span prototype numerical models of different spans. The methodology for conducted inquiry is described in detail in [12], but for the legibility and clarity of the paper, the most of import features will be repeated herein. Detailed analysis results presented in this paper showed that multiple-back up excitation had an unfavorable effect on the seismic behavior of analyzed bridges. Hence, this miracle should be considered in the design of bridges of similar layouts.

2. Paradigm Bridges

2.1. Bridge Prototypes Description

Numerical models correspond bridges of layout, material properties and cross-sections dimensions that are verified for persistent design situations [35]. Analyzed bridges were of arch spans L = 100 one thousand, 200 m, 300 m and 400 m with the rising to span ratio of 0.two (Figure 3) and shaped as catenary with abiding springing to crown load ratio. Deck spans were between 28 one thousand and 33.v m for all bridges. Three different sets of span layouts were analyzed in order to investigate the influence of dynamic properties of the structural organisation on the seismic response to multiple-back up excitation. In the beginning set up, the connection betwixt spandrel columns and the superstructure is hinged (provided past fixed bearings), the connection is fixed in the second set, while in the tertiary one information technology is too monolithic but the arch is additionally stiffened (using large cross section) in gild to clarify the influence of the arch stiffness on bridge response. Information technology was assumed that superstructure is connected to abutments by longitudinally movable bearings. Bridges are founded on a proficient-quality rock (corresponding to basis blazon A according to Eurocode 8 [36]). It is important to mention that bridges with different site weather condition were not studied and local site effect was non accounted for.

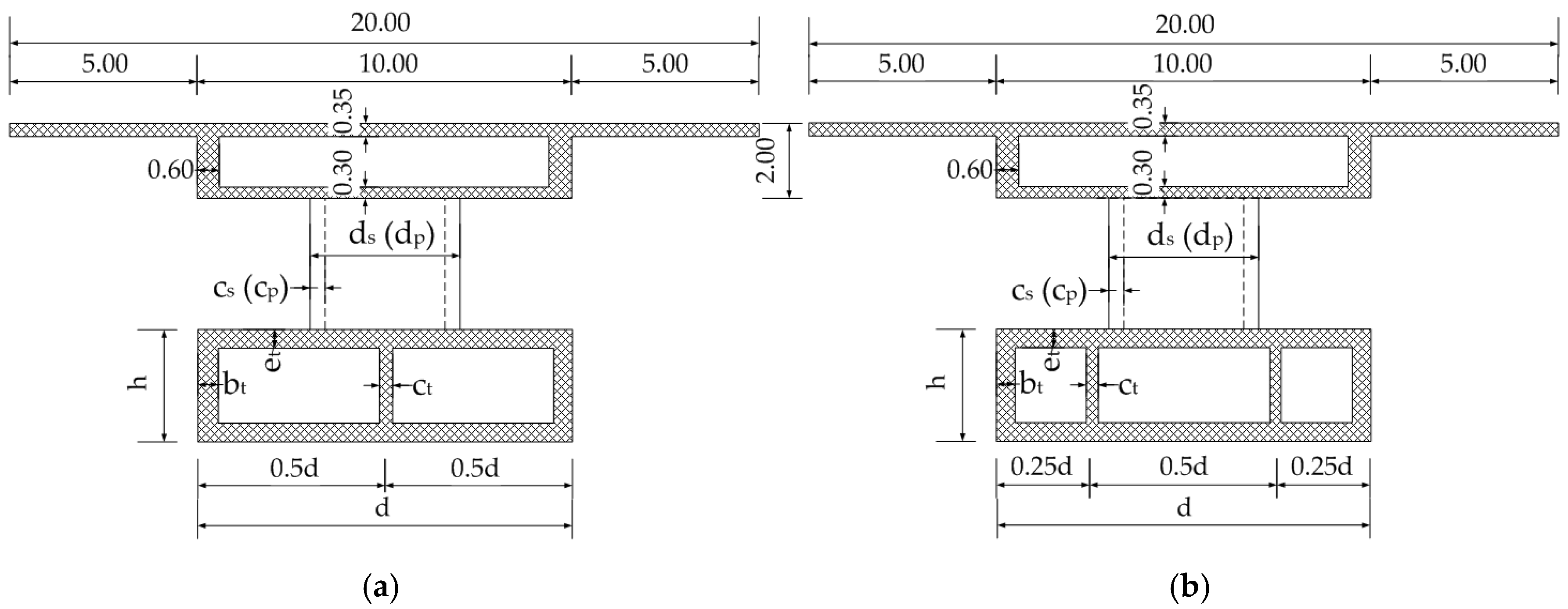
Figure 4 presents cantankerous sections of the span. The superstructure, spandrel columns, portal columns and arches are of cell-box blazon cross sections with constant dimensions given in Table 1. The designed concrete grade for the arch and superstructure is C45/55 and C35/45 for the columns [37]. Diaphragms are placed inside the arch nether spandrel columns. Their width is equal to the width of spandrel columns that they back up. The arch is connected to arch abutments past a diaphragm.

2.2. Numerical Modelling Strategies

Two-dimensional beam finite-element models were created for all bridge prototypes, with precise geometry and advisable spatial and time discretization of the problem, essential for calculation of loftier-frequency vibration modes [38].

Influence of geometric non-linearity was investigated in this research. This issue takes into business relationship increase of stiffness for elements subjected to a tension forcefulness and reduction of stiffness for elements subjected to a compression forcefulness ("softening" of structural elements), such as the arch. In the first case, numerical models for dynamic analysis were determined in the classical way, non taking into account the alter in the stiffness matrix due to expressionless loads action. In the second case, the analysis was performed using the stiffness matrix inherited from geometric non-linear staged construction pattern. The results from the ii cases were compared (dynamical properties, internal forces and displacements for the vertical load and for i case of multiple-support excitation (MSE)) and the differences were less than 10%. Hence, this issue was excluded in further analyses to MSE.

Cloth nonlinearity of the bridge cantankerous sections was not accounted for, every bit it was causeless that all load-begetting bridge elements respond in the rubberband range. Arch response is mostly non-ductile due to high thrust [39]. The energy loss in elastic range was simulated past Rayleigh damping wherein the damping of the first mode and the mode for which the modal participating mass ratio exceeds ninety% is assumed with the value of 5%. The Ritz vectors determined from inertia loads (mass for unit acceleration) forth two directions were used instead of classic eigenvectors. This avoids the negative property of eigen-value problem where eigen-modes are generated contained of the load type, so many eigen-vectors contribute very picayune or nothing to total active mass of the structure. The latter means that they are orthogonal or almost orthogonal to inertia loads. Therefore, an approach to avoid this phenomenon in numerical models is the application of Ritz-vectors, determined from inertia forces acting on the structure. In other words, displacements from these loadings represent the starting vector for the iterative procedure for calculating appropriate Ritz vibration vectors. Fifty Ritz vectors were determined in all numerical models, to obtain static and dynamic modal load participating coefficients of almost 100% in translational directions. For comparing, more double of classical eigen-vectors would have to be adamant to obtain approximately the aforementioned values of static and dynamic modal load contributions. If the loads are proportional to mass of the structure, contribution coefficients are in accordance with the total contribution coefficient of modal masses. Information technology should be noted, though, that for many Ritz vectors a very precise numerical model is mandatory, to minimize the discretization fault in determining loftier oscillation modes (with many zero points), necessary for analysis of structures to MSE, to acceptable level. The algorithm for the generation of Ritz vectors may exist found in [38].

As bridges are founded on rock, supports were modeled accordingly as springs of large stiffness. Abutments were not considered in numerical models.

Diaphragms placed inside the arch and those most abutments are not explicitly modelled, but their weight is taken into account. Boosted expressionless load acting on the superstructure includes all bridge equipment and pavement layers.

All numerical models were created and analyzed in Sap2000 software [xl], while the benchmark examples of the bridge of 100 m bridge were analyzed in Wolfram Mathematica [41] and Seismostruct [42]. Ane of the benchmark examples was presented in [12].

3. Methodology

3.i. Model of Spatial Variability of Ground Movement

The ground motility spatial variability is ofttimes probabilistically described using the space-fourth dimension random field of ground motion, with data obtained from the series of dumbo instrument arrays. Thus, this model tin be expressed through cross-power spectral density of the motions S(ξ_jk ,ω) = S(ω)·γ_jk (ξ_jk ,ω) where Due south(ω) is the power spectral density function of the motions, ξ_jk is the altitude of supports j and k, and γ_jk (ξ_jk ,ω) is the complex coherency. The circuitous coherency γ_jk (ξ_jk ,ω) for each frequency range contains the aamplitude term representing coherency loss |γ_jk (ξ_jk ,ω)| and the phase term θ_jk (ξ_jk ,ω) representing the moving ridge-passage effect.

The coherency loss is usually described by ways of the lagged coherency, which is the measure out of linear statistical dependence between seismic motions. For the perfectly linearly dependent processes the value is one, while it is zero for the completely independent processes. It is expected that at short distances and at low frequencies the motions will exist similar, while for big distances and at large frequencies the motions volition become uncorrelated [8].

Near lagged coherency functions accept been obtained empirically and semi-empirically using recorded information at strong motion arrays. Some of the empirical functions, developed mostly from the SMART-1 array, are those of Loh and Lin [43], Hao et al. [44], Abrahamson et al. [45], and Harichandran and Vanmarcke [46]. The functional form of semi-empirical models is analytically based, but parameters are evaluated from recorded data. Some of them are those proposed past Somerville et al. [47], Der Kiureghian [48] and Luco and Wong [49].

The selection of coherency model significantly affects the seismic response of structures subjected to multi-support excitation [7]. Hence, the recommendations for choosing the appropriate model from a big number available are necessary. The comprehensive discussion on this topic is presented in [8], where simulations of the motions from the two models very mutual in engineering applications, those of Harichandran and Vanmarcke [46] and of Luco and Wong [49], are compared. An important consideration in the selection of the coherency model is the site classification. The lagged coherency at rock sites has a flatter exponential decay than the lagged coherency at the softer soil sites. Co-ordinate to [7], coherency models at rock sites are express. Abrahamson [50] proposed an empirical coherency model for rock sites based on recordings at the Pinyon Flat array. Luco and Wong coherency model with a range of slower exponential decays, compatible with the trend of recorded data, can also be used as representative for the coherency at stone sites. Therefore, in this study the loss of coherency was modelled using this function, given by the expression:

$$\left|{\gamma }_{jk}({\xi }_{jk},\omega )\right|={\mathrm{east}}_{}^{-{\alpha }^2{\omega }^{\mathrm{ii}}{\xi }_{j\mathrm{chiliad}}{}^2}$$

(ane)

in which parameter α controls the exponential driblet of the coherency function with an increment of distance and frequency. Parameter α was taken with value of ii × x⁻⁴, the lowest value of those proposed by Luco and Wong, to exist appropriate for the stone site.

The moving ridge-passage consequence depends on the apparent velocity of the waves. According to Abrahamson [51], studies of motions recorded in several arrays showed that the credible velocity of S-waves is typically in the range 2.0–3.5 km/due south. Hence, the value of 2 km/due south was called in this study. It was assumed that seismic wave propagated from the left abutment as the reference station to the other bridge supports in the direction of the principal bridge axis.

Although the expansion of Kanai–Tajimi spectra [52] adult past Clough and Penzien [53] is usually selected every bit the spectral density function, in this written report the proposal by Kaul [54] was followed for generating fourth dimension-histories in order to reach matching with target spectra in fewer iterations:

$$S(\omega )=\frac{2\zeta }{\pi \omega }\cdot R\mathrm{Southward}{A}^2(\omega )\cdot \frac{1}{-2\ln (-\frac{\pi }{\omega T}\ln p)}$$

(ii)

where RSA represent to target spectra ordinates, ζ is the damping coefficient, T is duration of the generated records and p is probabilistic coefficient, normally ≥0.85 [54].

In this study, the Eurocode viii elastic pseudoacceleration spectrum of type 1 for ground type A [36] with superlative ground acceleration of 0.2 thousand was called equally the target response spectrum. Duration of the records was twenty south [15] and p was taken with the value of 0.85, in accord with [54].

3.2. Analysis Methods and Multiple-Support Analysis Cases

As already mentioned in the Introduction, the methods used in this study are in accordance with [12], but the most important features volition be summarized herein. Analysis methods include response spectrum method co-ordinate to Der Kiureghian and Neuenhofer (using Multiple Support Response Spectrum (MSRS) fortran code) [55,56], time-history method using generated records and simplified process for consideration of spatially variable seismic excitation proposed in Eurocode eight [57]. The cardinal data on these methods is presented in Figure 5, while the methods of generating records for time-history method volition be briefly elaborated beneath.

Ground-movement records needed for time-history method were generated using ii procedures. In the offset one, conditional simulation using spectral representation method proposed by Deodatis [58] was applied, simply with his extension to adapt the records to be compatible with the target spectra. In this report, the procedure was coded in Wolfram Mathematica according to the scheme presented in Figure 6.

The second process is unconditional simulation proposed by Vanmarcke et al. [59] in which a recorded ground motion is applied for generation of ground motions at other supports based on a spatial variability model. Basic input consisted of location of the supports, the spectral density function (SDF), the frequency-dependent spatial correlation office and the known basis move at support. The procedure was performed in the plan SIMQKE-II [60].

In improver to records generated by conditional and unconditional method, time-histories provided by seismic guidelines of New York Urban center Section of Transportation (NYCDOT) were also applied [61]. These are readily bachelor spatially-variable fourth dimension histories sets for grand-yr, 1500-year and 2500-year earthquake return periods. Each one of these three sets incorporates the effects of spatial variation forth 21 hypothetical piers on very difficult rock spaced at 100 thousand and extended over a directly line having a total length of 2 km. The formulation used for generation is according to Abrahamson [50]. NYCDOT motions were used for checks as they are not compatible with Eurocode spectrum. In total, thirteen ground motion sets were generated using the unconditional simulation, 7 using conditional simulation and 3 sets of prescribed motions were taken from the NYCDOT standards.

Elastic response spectra of recorded motions at the left abutment (for provisional simulation method) and spectra of generated motions using unconditional method and of prescribed motions past NYCDOT are presented in the left part of Figure vii. On the correct side of the aforementioned figure, one case set of displacement records at bridge supports is shown.

It is important to point out that, generally, the response of structures to MSE cannot be analyzed using the recorded accelerograms just, as a large number of simultaneously recorded time-histories at dissimilar distances, in different soils, of dissimilar magnitudes, etc., should exist available. As such seismic database does non exist, a procedure for generation of records must exist applied. For case, Eurocode eight [57] in its informative annex D related to MSE does not even mention the utilise of recorded motions in time-history analysis, but just the generated ones. Their number should be such as to yield stable estimates of the mean of the maximum responses of interest. Therefore, in this written report the assay was fabricated with the xx generated motions, excluding the NYCDOT ones.

Furthermore, in the part of the standard not directly related to MSE, where the fourth dimension-history representation is discussed, it is suggested that the advisable modified/faux records are used when the recorded ones with location-compatible characteristics are not bachelor. In every case, the average response spectra of the individual spectra of the used fourth dimension-histories should be non lower than one.iii times the 5% damped elastic response spectrum in the period range between 0.2T_one and 1.5 T₁, where T₁ denotes the fundamental period of the construction. In full general, when a three-dimensional assay is beingness carried out, the components of each pair of time-histories should be applied simultaneously.

The Hilber–Hughes–Taylor directly integration method with α = 0 (abbreviated to HHTα) was applied for numerical implementation of the time-history procedure. Information technology is of import to mention that very short fourth dimension steps were used, because of the application of displacement ground motility records (versus traditionally used acceleration records) [38].

Subsequently verification of numerical models, the post-obit seismic cases were analyzed:

• Case 1 (U): uniform ground excitation;

• Case 2 (WP): multiple-support excitation with time delay of the motions (wave-passage issue on perfectly coherent seismic waves);

• Case 3 (C): multiple-support excitation with the coherency loss (it is causeless that the velocity is approaching infinity);

• Case 4 (WPC): multiple-support excitation with WP and C.

four. Results

4.one. Dynamic Assay

In the following table (Table 2) the showtime 10 Ritz vectors and respective natural periods are presented. The showtime mode shape is antisymmetric for all analyzed bridges, with modal mass participation ratios in the longitudinal management ranging from l–lxx% for arches of 100 m span, 35–38% for 200 m spans, 33–35% for 300 m spans and 32% for 400 m spans. Second mode shape is symmetric for all analyzed bridges except for the bridge F100. The offset two style shapes of bridges with static system F are presented in Effigy 8.

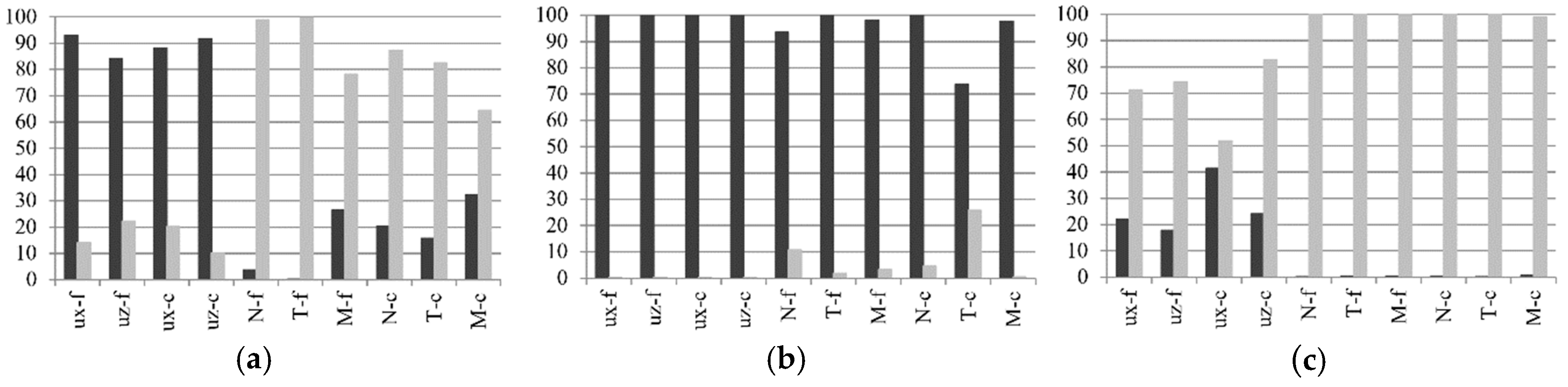
Elastic response spectrum from Eurocode 8 is presented in Figure 9, together with histogram of modal mass participation ratios larger than v% for all analyzed bridges. As the earthquake records were generated to conform to the prescribed spectrum, information technology is interesting to determine where are the modes with large contribution of mass located in relation to the seismic load. It should be pointed out that the spectrum values are given in units [m/s²] which are shown on the left vertical axis, while the modal mass participation ratios are in [%], shown on the right vertical axis. The unlike shades of colors have been used in histograms (blue for the modal mass participation ratios of 100 m span bridges, green for the 200 thou bridge bridges, red/pinkish for the 300 g span bridges and orange for the 400 one thousand span bridges).

iv.2. Seismic Analysis Accounting for Multiple-Back up Excitation Furnishings

Results are presented for the arch every bit the principal load-bearing chemical element. Arch sections in which axial strength (Northward), angle moment (M), shear forcefulness (T) and displacements (u_x and u_z) were analyzed include arch springings (p), quarter span (f) and curvation crown (c).

Firstly, the results of seismic analysis using the fourth dimension-history method volition be presented. The ratio of absolute values of tiptop response for the multiple-support and compatible excitations was adamant for each analyzed arch section and for each ready of time-histories (twenty in full, without NYCDOT motions) according to the expression:

$${\rho }_{\mathrm{ane}}=\frac{\mathrm{height}\mathrm{response}\mathrm{to}\mathrm{the}\mathrm{multi}-\mathrm{support}\mathrm{excitation}(\mathrm{C},\mathrm{WP}\mathrm{or}\mathrm{WPC})}{\mathrm{acme}\mathrm{response}\mathrm{to}\mathrm{the}\mathrm{compatible}\mathrm{excitation}\left(\mathrm{U}\right)}$$

(3)

For ratios ρ ₁ > 1, multiple-support excitation (MSE) has a detrimental consequence on the seismic response in relation to the uniform excitation. The arithmetics mean of all the ratios for each set of time-histories and for each instance of multiple-support excitation was calculated, and the standard deviation was σ < i/3 ρ _ane in all analyzed cases.

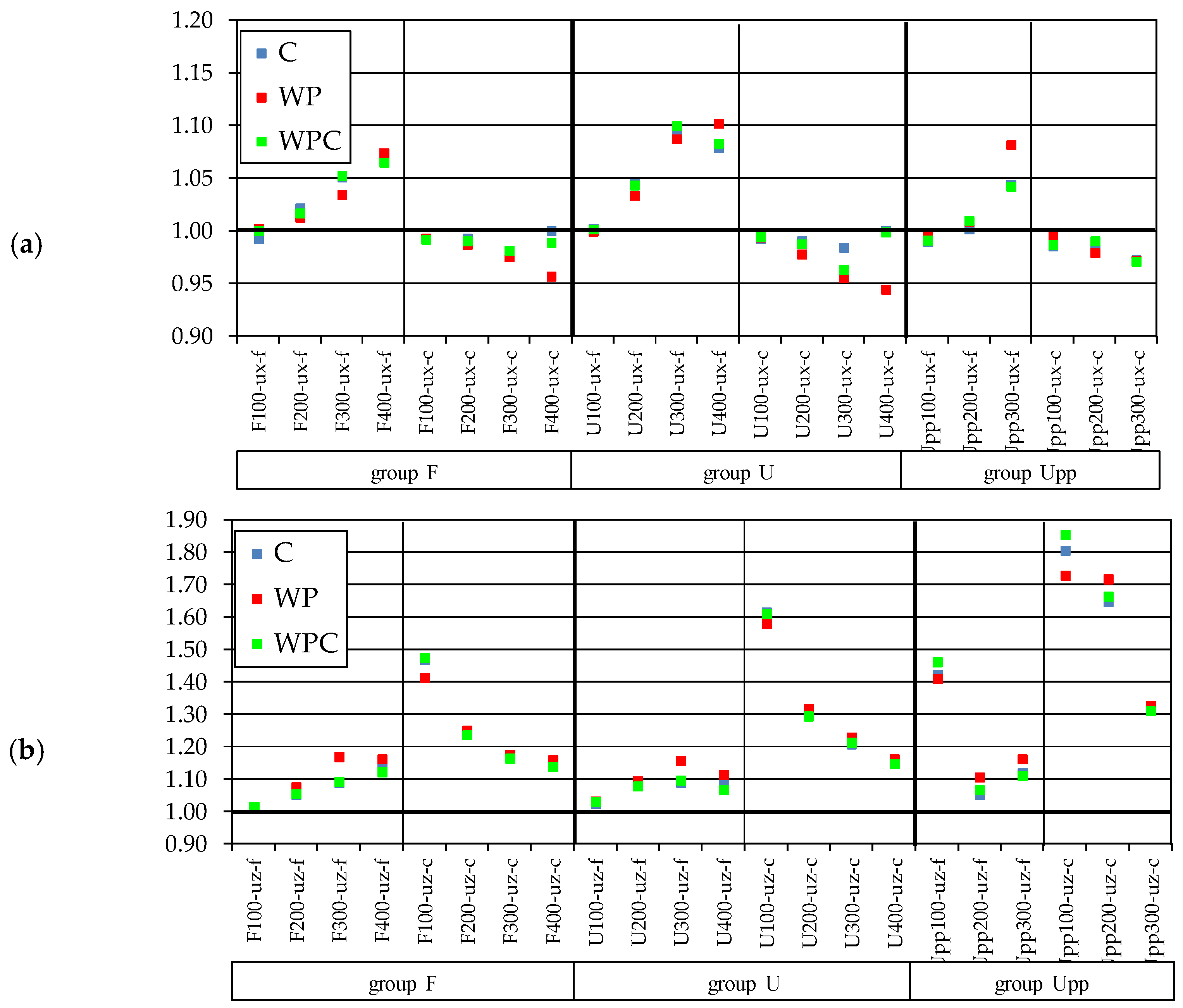
The boilerplate ratios ρ _ane for all analyzed cases of MSE are shown in Effigy ten and Figure 11, for all analyzed bridges grouped by static system.

It may be observed that the nigh detrimental upshot of MSE appears for the crown bending moment of the bridge U100 for the WPC case, with the ratio of three.63. Regarding the displacements, the most unfavorable response occurs due to WPC case for the crown vertical displacement of the bridge Upp100, amounting to 1.86. Such a detrimental values occurring for MSE in the arch crown take been anticipated, because both symmetric and antisymmetric modes are excited. For compatible excitation symmetrical mode, shapes are not excited, and then the crown of the symmetrical arch bridge does non undergo a vertical deportation (Figure 2) due to seismic activity. Bending moments in the springings occurring for uniform excitation are adequate for all bridges, except the very potent ones (Upp) where the largest ratio amounts to one.35 for the WPC case. Even so, the values at quarter span due to uniform excitation are unacceptable and the ratios are up to i.45 for the WP case of the bridge Upp300.

Further unfavorable responses may be observed for axial forces in all analyzed sections of all the bridges, with the crown beingness the virtually critical one with ratios upward to 1.68 of the bridge U200. Information technology may be observed that in near all analyzed cases the virtually unfavorable is the WP instance. The unfavorable response of axial forces obtained is in accordance with the results presented in [29,30,33].

Regarding the shear forces, the most detrimental response of MSE may exist observed at the quarter span of the strong bridges amounting to 1.42 for the WPC case of the bridge Upp100. For the shear force in the arch crown the uniform excitation is on the condom side.

All longitudinal displacements are in order of ±ten%, so disregarding MSE is acceptable.

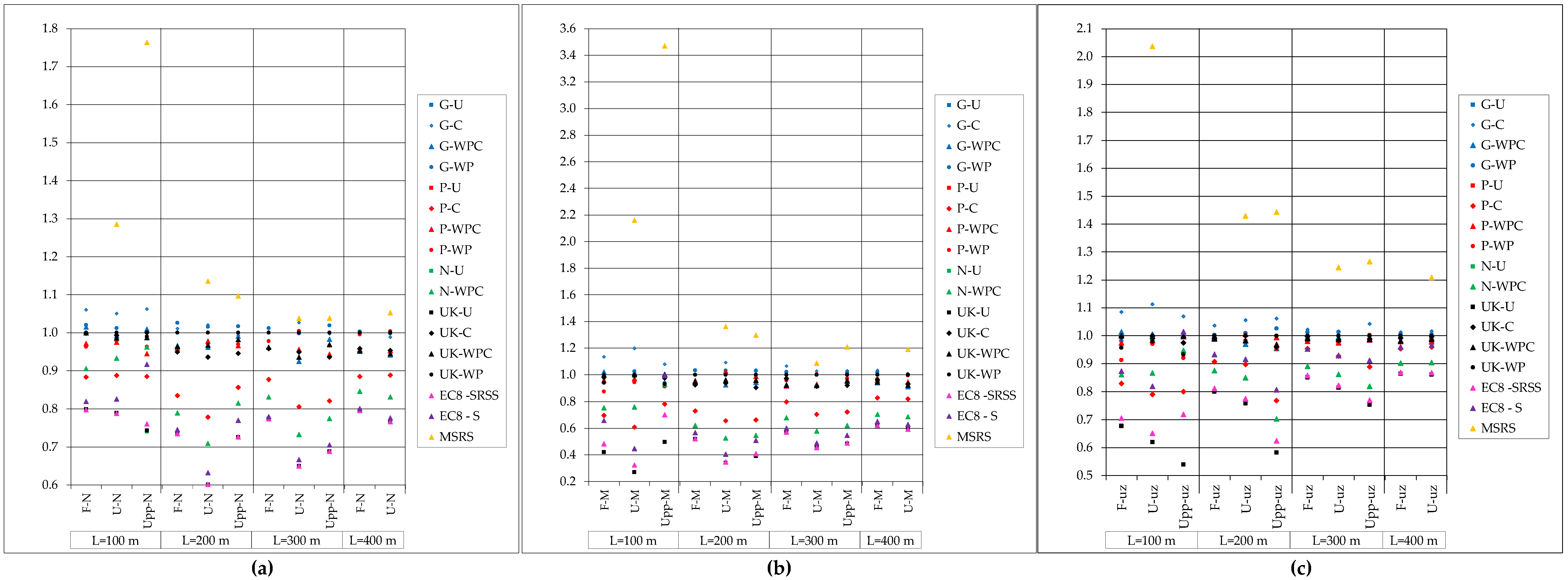
Following the results of fourth dimension-histories, the ratio ρ _two of the accented values of peak response for the multiple-support cases calculated using unlike methods and the most detrimental case obtained by the time-history method using all generated records (Britain) was determined for each analyzed curvation section. Therefore, the average ratios ρ ₂ are presented in Figure 12 and Effigy 13 in order to compare results of unlike analysis methods. Results of time-history method are given for records generated using different methods (denoted by G for unconditional simulation, P for conditional simulation, Due north for NYCDOT motions and United kingdom of great britain and northern ireland for all generated motions excluding NYCDOT). The response spectrum method for multiple-support excitation is labelled as MSRS (analyses exclude the bridges of static system F). The cases of simplified method according to Eurocode 8 are labelled as EC8-SRSS for the case in which the combination of the well-nigh unfavorable dynamic response and the most unfavorable furnishings obtained by quasi-static analysis is calculated using the SRSS dominion, while the approach in which this combination is obtained by summing absolute values of the dynamic and quasi-static response is labelled EC8-S.

Results prove that simplified process proposed past EC8 more often than not underestimates the response of analyzed arch bridges to MSE, regardless of bridge. At quarter span, the ratios ρ _ii of the internal forces are in the range of 0.67 (0.72 for EC8-Due south) to 0.94 for EC8-SRSS (ane.28 for EC8-S) for the angle moment of the span Upp100. The vertical displacements are in relatively good agreement with the reference values (in the range of 0.82 to 0.94 for EC8-SRSS and 0.97 to 1.xiv for EC8-Southward). At the curvation crown, the values obtained by both EC8 cases are far below the reference values, with the lowest ratio amounting to 0.32 occurring for angle moments in the bridge U100. Vertical displacements are in the range of 0.62 to 0.87 for EC8-SRSS and 0.81 to 1.01 for EC8-S for all bridges. Results are not presented for the arch springing every bit they follow the same tendency equally those commented above.

Regarding the records used in the time-history method, information technology may be observed that all values obtained using records from NYCDOT are significantly lower than all other values, which has been expected as the elastic response spectrum prescribed past NYCDOT is more favorable for analyzed bridges than that of EC8. The most detrimental values are calculated using the record generated using unconditional simulation, what has too been predictable accounting for the characteristics of the point, which cannot be considered realistic.

The MSRS method mostly gives conservative values for MSE. At quarter span, the values of the internal forces are in relatively skilful understanding (upwardly to ane.16), except for the span Upp100 where the ratio for axial strength amounts to i.49 and iii.73 for the bending moment. Vertical displacements are significantly overestimated for stiff bridges, especially for the bridge Upp100 where the ratio amounts to 5.4. At arch crown, the values obtained by MSRS are very dissimilar than the reference values, ranging from 0.5 to 3.65.

It is interesting to compare the pseudo-static and dynamic component of the response, in MSRS method, for two bridges of the aforementioned span merely unlike stiffness, U100 and Upp 100 (Figure 14a,b). Information technology may be observed that for the displacement of the bridge U100 the pseudo-static component prevails, while the dynamic ane is more than important for the internal forces. For very stiff bridge Upp100, pseudo-static component is more than important for all response values and it is the primary reason for very unfavorable response of this span to MSE. These components are also presented for a flexible bridge U400, where the dynamic component dominantly affects all the response values (Figure 14c). Information technology is repeated herein that the dynamic component of the response to MSE differs from the i to uniform excitation. These conclusions are in line with those obtained past Hao [23], who investigated circular arches and concluded that the responses of stiff arches are generally dominated by the quasi-static responses, while the dynamic responses dominate the flexible arch responses owing to a dynamic amplification result.

5. Discussion

5.1. Influence of Structural Dynamic Parameters and Bridge Length

The influence of dynamic properties of the system on response values cannot exist observed, except for the vertical displacements of the curvation crown where it is evident that within one group of curvation spans (for example, Fifty = 100 m) the unfavorable action of the MSE increases with the stiffness of the arrangement.

The detrimental issue of the MSE on the values of the bending moments and the longitudinal displacements of the quarter curvation more often than not increases with the increase of the span within the aforementioned static system. For all crown displacements, the opposite is true, then that increasing the span results in decreasing the unfavorable effect of MSE.

five.2. Influence of MSE Effects

Analyzing ratios ρ ₁ it may be observed that the moving ridge-passage outcome is in near cases more detrimental to the response than the loss of coherency. Exceptions occur for bridges F100 and Upp100. However, it should exist noted that when values obtained past calculation using records generated by unconditional and conditional simulation are analyzed separately, in many cases the almost unfavorable grade of MSE is that with the effect of coherence loss using records obtained by unconditional simulation calculations, while for the values obtained from calculations using records generated by provisional simulation, in near cases the most unfavorable course of MSE is the i with the influence of the moving ridge-passage.

Hence, the general trend of the behavior of the observed values cannot be determined and the results depend on the records used. Therefore, it is recommended that the blueprint analyses should include both considered MSE furnishings.

5.3. Influence of Assay Methods and Applied Ground-Motion Time-Histories

As previously mentioned, the largest average peak fourth dimension-history results obtained using generated records were assumed every bit the reference values for validation of all methods.

The simplified method proposed in EC8 systematically underestimates response values and, therefore, it is non suggested for the assay of like bridges. This conclusion is in accord with the findings of some other studies in which EC8 simplified method was applied. For case, in the recent study of the integral span [22], it was ended that EC8 arroyo provides results in the order of ±40–fifty% of the reference values, owing to the disability of the method to predict the contribution of higher modes every bit well as the location of structural elements which are favorably or unfavorably afflicted by spatially variable seismic deportment. The research presented in [xviii] dealt with the response of bridges to MSE and evaluation of EC8 provisions very comprehensively. The authors concluded that in some cases the provisions of the EC8 on the simplified method may be safely practical, but in other cases ignoring the effect of MSE or performing simplified calculations can significantly underestimate the actual seismic demand. In the study of an arch bridge response to multiple-support excitation presented in [33] the authors also suggested reexamining the limit for consideration of spatial variability effect in concrete arch bridges, proposed by Eurocode 8.

Moreover, the modification of the method in which the combination of the nigh adverse dynamic response with the most agin furnishings obtained past the quasi-static analyses is calculated by applying the sum of absolute values, applied also in [eighteen], cannot be recommended for the use since the response values are even so underestimated, with a few exceptions that cannot influence the method pick.

Information technology can exist observed that the response spectrum method MSRS does not accurately estimate the response of curvation bridges to MSE, with some values being significantly lower and some higher than the reference values, which is in line with the research presented in [62], proposing its modification. Therefore, begetting in mind besides the full general inapplicability of the method to any non-linear analysis, this method is not recommended for the calculation of similar bridges to MSE.

The utilize of earthquake records generated by unconditional simulation produces very conservative results, and information technology should be kept in mind that such "bogus" records are used because of the lack of recorded ones and they can never realistically ascertain an earthquake excitation. The reward of using such a simulation is that information technology simply and quickly generates a large number of records one time a calculation algorithm is made, which is useful for parametric analyses. The procedure of conditional simulation using recorded motions is more than demanding, because it is firstly necessary to find a series of appropriate records from a stiff-motion database with respect to the bridge location (which is not ever possible), taking into account the code rules and, if necessary, to process them (baseline correction and filtering). Then, for each selected record, the fourth dimension windows and the spectral power density function for each of these should be determined, taking care that the duration of each stationary fourth dimension window is twon since changed fast Fourier transforms are used in the simulation. It is axiomatic that it is very challenging to fully automatize such a process. Only after this initial selection and aligning procedure has been carried out tin the process of generating records for the other supports of the bridge be initiated. The records generated using this method retain the properties of the original recorded fourth dimension-histories (for example, the frequency content of the signal) so that they tin can more realistically define the earthquake excitation than the "artificial" records generated on the basis of a probabilistic model. Taking into account these findings, it is suggested that, depending on the problem itself (for example, pattern or theoretical parameter analyses), a record generation process should be selected. Information technology is further noted that special attention should exist paid to the processing of dispatch records, since displacement records are generally used in the analysis of the MSE upshot.

6. Conclusions

This study investigated the influence of multiple-support excitation on seismic beliefs of deck-type long-span reinforced concrete arch bridges. Results of the comprehensive analysis showed that applying a compatible seismic input at all bridge supports, as is commonly washed in technology practise, was not adequate for these bridges. In all studied cases, multiple-support excitation had a detrimental effect on some attribute of the arch bridge seismic response, regardless of bridge length (the minimal span was 100 g). Hence, it may be recommended that this phenomenon is included in seismic analysis of similar structures, even if it is not required past the engineering science design codes.

Both ground-motion effects acting separately or simultaneously proved to be very important, with their relative significance depending on response values, analyzed arch locations, and utilized earthquake time histories. Therefore, information technology is suggested that both MSE furnishings are considered in seismic analysis of similar bridges. It should be pointed out that deck arch bridges of long spans are commonly synthetic on rock sites, considering of the big arch thrust that needs to be transferred to the footing. Therefore, the effect of local-site atmospheric condition was not considered in addition to coherency loss and moving ridge-passage. However, if the bridge location is at uneven site with non-uniform conditions at dissimilar supports, this influence on footing move amplification and spatial variation should exist considered. A simplified approach would be to employ the process presented in this newspaper (Effigy 6), but to define different response spectra taking into account the soil category of different supports. Withal, one should bear in mind that the local site conditions have a much more complex outcome than the spectral modification prescribed by the lawmaking design spectra and thus, a more comprehensive arroyo to this effect may exist suggested, such equally that applied in e.g., [18,63]. Moreover, if the foundation interacts with the soil and the superstructure, thus significantly affecting the dynamic response of the bridge, this further complicates the analysis, and the state-of-the-art knowledge in geotechnical convulsion engineering and earthquake structural engineering should be practical accordingly. The soil–structure interaction may reduce the effect of multiple-support excitation past increasing the fundamental period of the construction and by introducing the dissipation of free energy at foundations level. Nonetheless, foundation rotations may induce large pseudo-static forces [64]. It was ended in [eighteen] that pregnant coupling exists between spatial variability, furnishings of local soil conditions and SSI furnishings, but their relative importance cannot exist easily assessed in accelerate.

In this research, no rule in response of bridges was apparent regarding the outcome of dynamic structural backdrop and arch span, with few exceptions. Comparison of the diverse methods showed that the most suitable analysis procedure was fourth dimension-history method, because other procedures proved to exist less accurate and considering of its general applicability. In particular, it was shown that simplified method proposed by valid European seismic codes systematically underestimates the MSE event, so it is not recommended for employ in engineering practice. EC8 rules, which specify that in the case of roughly compatible soil properties along the bridge, spatial variability must just be considered if the bridge length is larger than 400 k for rocky soils, cannot be safely used to analyze deck-reinforced concrete arch bridges. The other code deficiencies were as well observed, such as the lack of guidelines on selecting the coherency loss functions and credible wave velocities. These findings are corroborated by a recent paper [64] addressing these issues and, furthermore, by proposals of simplified differential displacement loading patterns for use in the seismic blueprint of bridges bookkeeping for MSE past the same authors [65], and we believe that the new generation of EC seismic standards should consider these studies.

Although presented conclusions have been drawn from a express-scope report of plane response of deck-type reinforced physical curvation bridges founded on rock sites, information technology is obvious that many gaps still exist in successful inclusion of MSE effect into the design standards and in providing guidelines that could exist useful and understandable to engineering professionals. Therefore, information technology may exist suggested to undertake more initiatives to investigate the effect of MSE on bridges of various types and materials, soil conditions and earthquake scenarios, using numerical procedures, only also experimental inquiry, as superior systems of multiple shaking tables have been installed in several research institutions worldwide.

Author Contributions

D.Fifty. initiated and supervised this written report. M.S.N. performed the core research (all numerical examples) and wrote the initial typhoon of the paper. J.A. and M.U. checked the results of the study, helped in information processing and revised the paper. All authors accept read and agreed to the published version of the manuscript.

Funding

This research was partially funded by Ministry building of Science, Educational activity and Sports of Republic of Croatia, under study Not-standard models of building structures, grant number 082-1201829-2166.

Acknowledgments

The authors would like to thank Section of Geophysics, Faculty of Science, University of Zagreb, for providing footing motions recorded on the Adriatic Coast and to colleagues from the Department of Structures, Faculty of Civil Applied science, University of Zagreb, who designed some of the bridges used for creating prototypes and supplied all span information necessary for the analyses.

Conflicts of Involvement

The authors declare no disharmonize of interest.

References

1. Gazetas, K.; Simeonov, V.; Reinhorn, A.Grand.; Buckle, I.G. Implications of Spatial Variation of Footing Motion on the Plummet of Sr14/I5 Southbound Separation and Overhead Bridge in the Northridge Earthquake. ACI Int. 1999, 187, 299–327. [Google Scholar]
2. Tzanetos, N.; Elnashai, A.Southward.; Hamdan, F.H.; Antoniou, S. Inelastic Dynamic Response of RC Bridges Subjected to Spatial Not-Synchronous Convulsion Motion. Adv. Struct. Eng. 2000, 3, 191–214. [Google Scholar] [CrossRef]
3. Yashinsky, M. Bridge Repairs Later the 1995 Kobe (Hyogo-ken Nanbu) Earthquake. In Lessons Learned Over Time—Learning From Earthquake Series, Volume III; Earthquake Engineering Enquiry Institute: Oakland, CA, USA, 2000. [Google Scholar]
4. Earthquake Engineering Inquiry Center. Seismological and Engineering Aspects of the 1995 Hyogoken-Nanbu (Kobe) Earthquake, Study No. UCB/EERC 95-10; Earthquake Engineering Inquiry Center, College of Engineering, Academy of California: Berkeley, CA, USA, 1995. [Google Scholar]
5. Bogdanoff, J.L.; Goldberg, J.Eastward.; Schiff, A.J. The issue of footing manual time on the response of long structures. Bull. Seismol. Soc. Am. 1965, 55, 627–640. [Google Scholar]
6. Bolt, B.A.; Loh, C.H.; Penzien, J.; Tsai, Y.B.; Yeh, Y.T. Preliminary Report on the SMART 1 Potent Motility Assortment in Taiwan, Study No. UCB/EERC-82/13; Earthquake Technology Research Center, College of Engineering, University of California: Berkeley, CA, Us, 1982. [Google Scholar]
7. Zerva, A. Spatial Variation of Seismic Ground Motions: Modeling and Engineering Applications; CRC Press: Boca Raton, FL, U.s., 2009. [Google Scholar]
8. Zerva, A.; Zervas, Five. Spatial variation of seismic ground motions: An overview. Appl. Mech. Rev. 2002, 55, 271. [Google Scholar] [CrossRef]
9. Harichandran, R.S. Spatial Variation of Earthquake Footing Motion, What is it, How do We Model it, and What are Its Applied science Implications; Michigan State University: East Lansing, MI, USA, 1999. [Google Scholar]
10. Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, Us, 1996. [Google Scholar]
11. Reiter, L. Earthquake Adventure Analysis: Issues and Insights; Columbia University Press: New York, NY, USA, 1990. [Google Scholar]
12. Savor Novak, M.; Lazarević, D.; Atalić, J. Influence of spatial variability of ground motion on seismic response of bridges. Gradevinar 2015, 67, 943–957. [Google Scholar]
13. Monti, Yard.; Nuti, C.; Pinto, P.East. Nonlinear response of bridges under multi support excitation. J. Struct. Eng. ASCE 1996, 122, 1147–1159. [Google Scholar] [CrossRef]
14. Lupoi, A.; Franchin, P.; Pinto, P.E.; Monti, 1000. Seismic pattern of bridges accounting for spatial variability of ground motion. Earthq. Eng. Struct. Dyn. 2005, 34, 327–348. [Google Scholar] [CrossRef]
15. Shinozuka, G.; Saxena, V.; Deodatis, G. Effect of Spatial Variation of Basis Move on Highway Structures, Technical Written report MCEER 00 0013; Multidisciplinary Center for Convulsion Engineering Enquiry (MCEER), Academy at Buffalo, State Academy of New York: Buffalo, NY, Us, 2000. [Google Scholar]
16. Burdette, N.J.; Elnashai, A.S.; Lupoi, A.; Sextos, A.M. The Effect of Asynchronous Earthquake Motion on Complex Bridges; Mid-America Earthquake Center, Department of Civil Engineering at the University of Illinois at Urbana-Champaign: Urbana, IL, Usa, 2006; pp. one–28. [Google Scholar]
17. Sextos, A.Grand.; Kappos, A.J. Evaluation of seismic response of bridges nether asynchronous excitation and comparisons with Eurocode 8-two provisions. Bull. Earthq. Eng. 2009, seven, 519–545. [Google Scholar] [CrossRef]
18. Sextos, A.G.; Kappos, A.J.; Pitilakis, K.D. Inelastic dynamic analysis of RC bridges accounting for spatial variability of basis motion, site effects and soil-structure interaction phenomena. Part two: Parametric study. Earthq. Eng. Struct. Dyn. 2003, 32, 629–652. [Google Scholar] [CrossRef]
19. Sextos, A.; Karakostas, C.; Lekidis, V.; Papadopoulos, South. Multiple support seismic excitation of the Evripos bridge based on gratis-field and on-structure recordings. Struct. Infrastruct. Eng. 2015, 11, 1510–1523. [Google Scholar] [CrossRef]
20. Dumanogluid, A.A.; Soyluk, K. A stochastic assay of long span structures subjected to spatially varying footing motions including the site-response effect. Eng. Struct. 2003, 25, 1301–1310. [Google Scholar] [CrossRef]
21. Adanur, Due south.; Altunişik, A.C.; Soyluk, K.; Bayraktar, A.; Dumanoğlu, A.A. Multiple-support seismic response of Bosporus Suspension Bridge for diverse random vibration methods. Case Stud. Struct. Eng. 2016, 5, 54–67. [Google Scholar] [CrossRef]
22. Özcebe, A.Grand.; Smerzini, C.; Bhanu, V. Insights into the Consequence of Spatial Variability of Recorded Earthquake Ground Motion on the Response of a Bridge Construction. J. Earthq. Eng. 2018, ane–27. [Google Scholar] [CrossRef]
23. Hao, H. Ground-Motion Spatial Variation Effects on Circular Arch Responses. J. Eng. Mech. ASCE 1994, 120, 2326–2341. [Google Scholar] [CrossRef]
24. Huang, C.S.; Teng, T.J.; Yeh, C.H.; Chi, C.H. Transient Response of Circular Arches for Base Excited Motions. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996; Pergamon: Oxford, U.k., 1996; p. 240. [Google Scholar]
25. Su, L.; Dong, Due south.; Kato, Southward. Seismic pattern for steel trussed arch to multi-support excitations. J. Constr. Steel Res. 2007, 63, 725–734. [Google Scholar] [CrossRef]
26. Harichandran, R.South.; Hawwari, A.; Sweidan, B.N. Response of Long-span Bridges to Spatially Varying Basis Motility. J. Struct. Eng. 1996, 122, 476–484. [Google Scholar] [CrossRef]
27. Soyluk, Thousand. Comparison of random vibration methods for multi-back up seismic excitation analysis of long-bridge bridges. Eng. Struct. 2004, 26, 1573–1583. [Google Scholar] [CrossRef]
28. Dusseau, R.A.; Wen, R.1000. Seismic Response of Deck-type Curvation Bridges. Earthq. Eng. Struct. Dyn. 1989, 18, 701–715. [Google Scholar] [CrossRef]
29. Kawashima, K.; Mizoguti, A. Seismic Response of a Reinforced Concrete Curvation Bridge. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 Jan–4 February 2000; New Zealand Society for Convulsion Engineering: Upper Hutt, New Zealand, 2000; p. 1824. [Google Scholar]
30. Zanardo, G.; Pellegrino, C.; Bobisut, C.; Modena, C. Performance Evaluation of Short Span Reinforced Concrete Curvation Bridges. J. Bridg. Eng. ASCE 2004, nine, 424–434. [Google Scholar] [CrossRef]
31. Savour, Yard.; Lazarevic, D.; Atalic, J. Influence of spatial variability of basis motion on response of big concrete arch bridges. In Proceedings of the IABSE-IASS Symposium, London, UK, 20–23 September 2011; Hemming Group Express: London, UK, 2011; p. 160. [Google Scholar]
32. McCallen, D.; Noble, C.; Hoehler, M. The Seismic Response of Concrete Curvation Bridges with Focus on the Bixby Creek Bridge, California, UCRL—ID—134419; Lawrence Livermore National Laboratory for California Department of Transportation: Livermore, CA, USA, 1999. [Google Scholar]
33. Álvarez, J.J.; Aparicio, A.C.; Jara, J.One thousand.; Jara, 1000. Seismic assessment of a long-bridge arch span considering the variation in centric forces induced by earthquakes. Eng. Struct. 2012, 34, 69–80. [Google Scholar] [CrossRef]
34. Papadopoulos, South.P.; Sextos, A.G. On the Excitation of Higher Modes of Long Bridges Due to Spatial Variability of Earthquake Basis Move; Innov. Bridg. Soil-Bridge Collaborate. (IBSBI): Athens, Greece, 2011. [Google Scholar]
35. Savor, Z. New Contribution to Development of Arch Bridges. Ph.D. Thesis, Faculty of Ceremonious Applied science, Academy of Zagreb, Zagreb, Republic of croatia, 2005. [Google Scholar]
36. CEN. Eurocode 8: Design of Structures for Earthquake Resistance—Part one: Full general Rules, Seismic Actions and Rules for Buildings; CEN European Committee for Standardisation: Brussels, Kingdom of belgium, 2004. [Google Scholar]
37. CEN. Eurocode two: Pattern of Concrete Structures—Part 1-i: General Rules and Rules for Buildings; CEN European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
38. Wilson, E.L. Three-Dimensional Static and Dynamic Analysis of Structures A Physical Approach with Emphasis on Earthquake Engineering; Computers and Structures, Inc.: Berkeley, CA, United states, 2002. [Google Scholar]
39. Priestley, M.J.N.; Seible, F.; Calvi, One thousand.1000. Seismic Blueprint and Retrofit of Bridges; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
40. CSI. CSI Assay Reference Manual for SAP2000, Condom and CSiBridge; Computers & Structures: Berkeley, CA, USA, 2010. [Google Scholar]
41. Mathematica; Version 10.0; Wolfram Research, Inc.: Champaign, IL, USA, 2010.
42. Seismostruct; Version half dozen; Seismosoft Ltd.: Pavia, Italy, 2012.
43. Loh, C.H.; Lin, Southward.G. Directionality and simulation in spatial variation of seismic waves. Eng. Struct. 1990, 12, 134–143. [Google Scholar] [CrossRef]
44. Hao, H.; Oliveira, C.S.; Penzien, J. Multiple-station ground motion processing and simulation based on smart-1 array data. Nucl. Eng. Des. 1989, 111, 293–310. [Google Scholar] [CrossRef]
45. Abrahamson, Northward.A.; Schneider, J.F.; Stepp, J.C. Spatial variation of stiff ground motility for use in soil-construction interaction analyses. In Proceedings of the quaternary United states-National Conference on Convulsion Technology, Palm Springs, CA, USA, 20–24 May 1990; pp. 317–326. [Google Scholar]
46. Harichandran, R.S.; Vanmarcke, E.H. Stochastic variation of earthquake ground move in space and time. J. Eng. Mech. 1986, 112, 154–174. [Google Scholar] [CrossRef]
47. Somerville, P.Chiliad.; McLaren, J.P.; Saikia, C.K.; Helmberger, D.5. Site-specific estimation of spatial incoherence of strong ground motion. In Convulsion Engineering and Soil Dynamics Ii-Recent Advances in Basis Move Evaluation; Von Thun, J.L., Ed.; ASCE: New York, NY, U.s., 1988. [Google Scholar]
48. Der Kiureghian, A. A coherency model for spatially varying footing motions. Earthq. Eng. Struct. Dyn. 1996, 25, 99–111. [Google Scholar] [CrossRef]
49. Luco, J.E.; Wong, H.L. Response of a rigid foundation to a spatially random ground motion. Earthq. Eng. Struct. Dyn. 1986, xiv, 891–908. [Google Scholar] [CrossRef]
50. Abrahamson, N.A. Hard Rock Coherency Functions Based on the Pinyon Flat Assortment Information; Electric Power Research Institute: Palo Alto, CA, USA, 2007. [Google Scholar]
51. Abrahamson, N.A. Spatial Variation of Multiple Back up Inputs. In Proceedings of the First U.S. Seminar, Seismic Evaluation and Retrofit of Steel Bridges, Berkeley, CA, United states, eighteen October 1993. [Google Scholar]
52. Tajimi, H. A Statistical Method of Determining the Maximum Response of a Building Construction during an Convulsion. In Proceedings of the 2nd World Briefing on Convulsion Engineering science, Tokyo and Kyoto, Japan, 11–18 July 1960; pp. 781–797. [Google Scholar]
53. Clough, R.W.; Penzien, J. Dynamics of Structures, 2nd ed.; McGraw-Hill, Inc.: New York, NY, United states of america, 1993. [Google Scholar]
54. Kaul, M.K. Stochastic characterization of earthquakes through their response spectrum. Earthq. Eng. Struct. Dyn. 1978, 6, 497–509. [Google Scholar] [CrossRef]
55. Der Kiureghan, A.; Neuenhofer, A. Response spectrum method for multi-back up excitations. Earthq. Eng. Struct. Dyn. 1992, 21, 713–740. [Google Scholar] [CrossRef]
56. Der Kiureghian, A.; Keshishian, P.; Halabian, A.M. Multiple Support Response Spectrum Analysis of Bridges Including the Site-Response Effect & the MSRS Code 1997, Report No. UCB/EERC-97/02; Earthquake Engineering science Research Center, Higher of Engineering, University of California: Berkeley, CA, The states, 1997. [Google Scholar]
57. CEN. Eurocode viii: Design of Structures for Convulsion Resistance—Role 2: Bridges; CEN European Commission for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
58. Deodatis, Thousand. Non-stationary stochastic vector processes: Seismic footing motion applications. Probabilistic Eng. Mech. 1996, 11, 149–167. [Google Scholar] [CrossRef]
59. Vanmarcke, E.H.; Heredia-Zavoni, E.; Fenton, G.A. Conditional Simulation of Spatially Correlated Earthquake Ground Motility. J. Eng. Mech. ASCE 1993, 119, 2333–2352. [Google Scholar] [CrossRef]
60. Vanmarcke, E.H.; Fenton, G.A.; Heredia-Zavoni, East. SIMQKE-Ii, Conditioned Earthquake Ground Motion Simulator, User's Manual 2.i; Princeton University: Princeton, NJ, The states, 1999. [Google Scholar]
61. New York City Department of Transportation. Multiple Back up Motions Time-Histories; NYC DOT: New York, NY, Us, 2004.
62. Shen, J.; Li, R.; Shi, J.; Zhou, Chiliad. Modified multi-back up response spectrum analysis of structures with multiple supports under incoherent ground excitation. Appl. Sci. 2019, 9, 1744. [Google Scholar] [CrossRef]
63. Bi, K.; Hao, H. Modelling and simulation of spatially varying earthquake basis motions at sites with varying conditions. Probabilistic Eng. Mech. 2012, 29, 92–104. [Google Scholar] [CrossRef]
64. Falamarz-Sheikhabadi, G.R.; Zerva, A. Ii uncertainties in simulating spatially varying seismic ground motions: Incoherency coefficient and credible propagation velocity. Bull. Earthq. Eng. 2018, 16, 4427–4441. [Google Scholar] [CrossRef]
65. Falamarz-Sheikhabadi, M.R.; Zerva, A. Simplified displacement loading patterns for incorporation of spatially variable ground motions in bridge seismic design codes. J. Bridge Eng. 2017, 22, 04017010-one–04017010-14. [Google Scholar] [CrossRef]

Figure 1. Primary forms of spatial variability of ground motion [12].

Effigy one. Principal forms of spatial variability of footing motion [12].

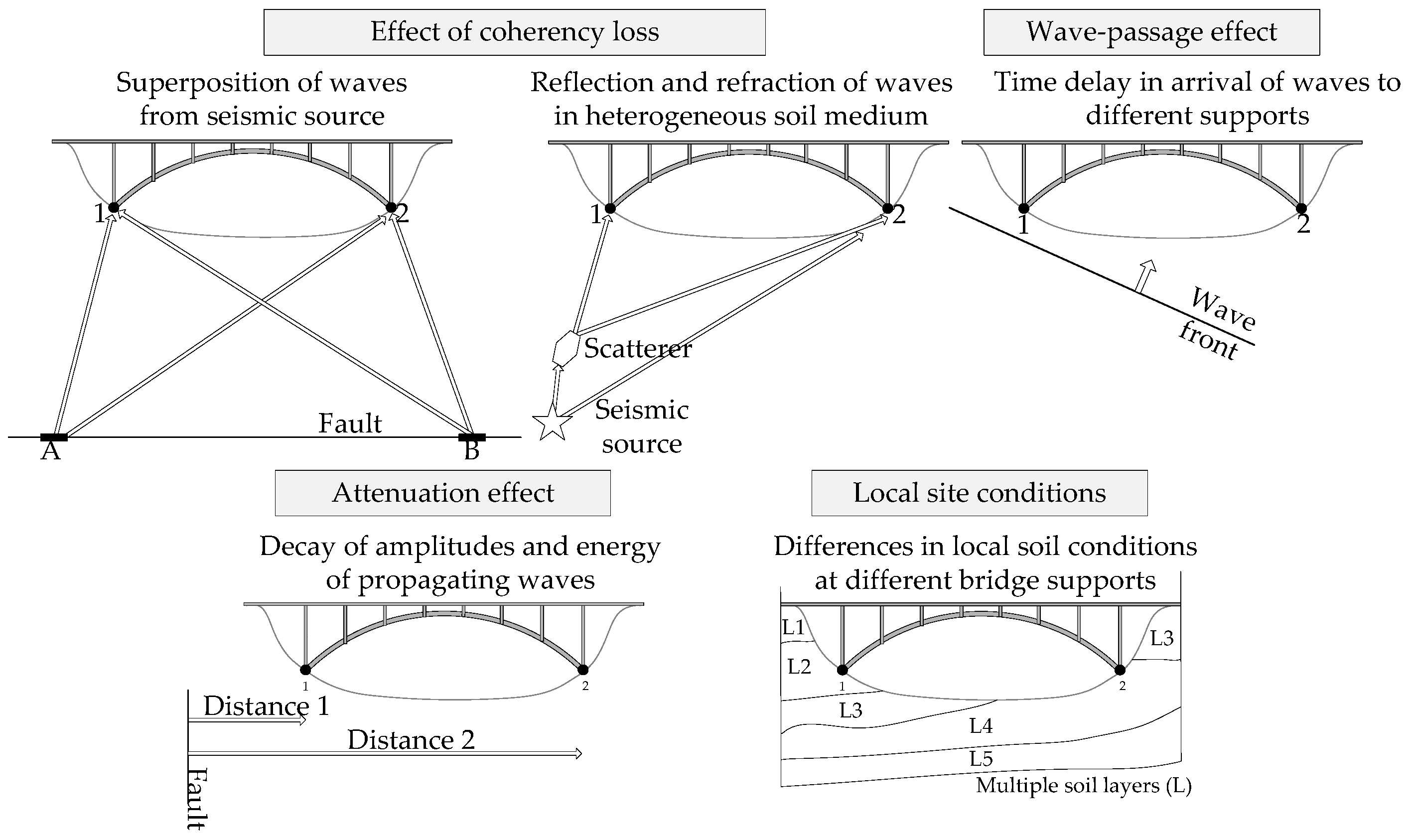
Figure 2. Relative arch displacements due to the uniform and multiple-support excitation [10].

Figure 2. Relative curvation displacements due to the uniform and multiple-support excitation [10].

Effigy iii. Layout of analyzed bridges.

Figure 3. Layout of analyzed bridges.

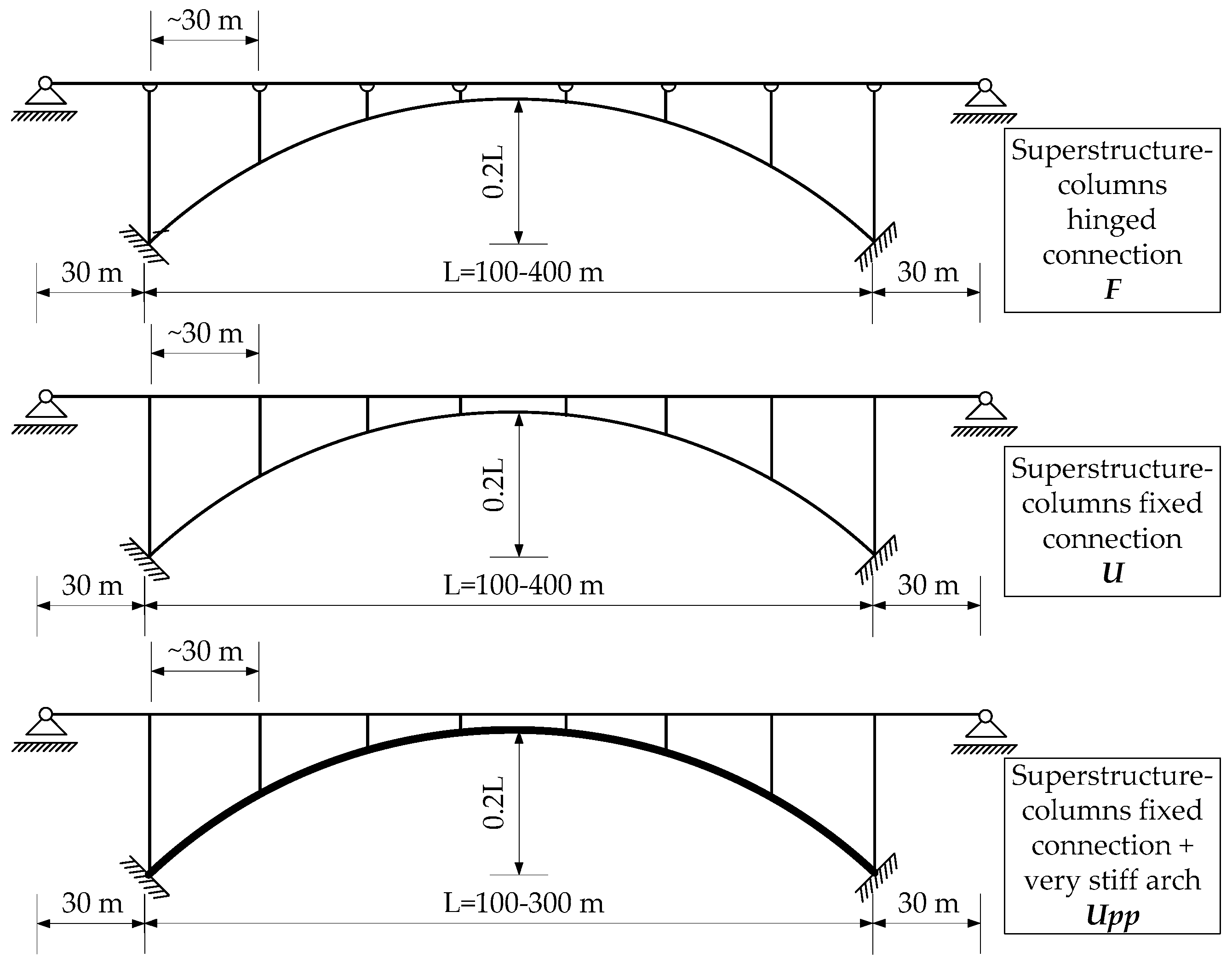
Figure 4. Cross sections of the bridges: (a) Spans 50 = 100 and 200 thousand; (b) Spans L = 300 and 400 m.

Figure four. Cross sections of the bridges: (a) Spans L = 100 and 200 m; (b) Spans L = 300 and 400 m.

Effigy 5. Analysis methods applied in this study.

Figure five. Analysis methods applied in this study.

Figure 6. Scheme of iteration procedure for generating seismic motions compatible with target response spectrum.

Figure half-dozen. Scheme of iteration procedure for generating seismic motions compatible with target response spectrum.

Figure 7. Elastic response spectra (ERS) and displacement fourth dimension-histories (DTH): (a) ERS of recorded motions at L = 0 1000 for conditional method; (b) DTH of the record 004674; (c) ERS of all generated motions using unconditional method; (d) DTH of one fix of motions; (due east) ERS of ane set of motions prescribed by New York City Department of Transportation (NYCDOT); (f) DTH of 1 fix of motions prescribed by NYCDOT.

Figure vii. Elastic response spectra (ERS) and displacement fourth dimension-histories (DTH): (a) ERS of recorded motions at Fifty = 0 grand for conditional method; (b) DTH of the record 004674; (c) ERS of all generated motions using unconditional method; (d) DTH of i set of motions; (e) ERS of i set of motions prescribed by New York City Department of Transportation (NYCDOT); (f) DTH of one set of motions prescribed by NYCDOT.

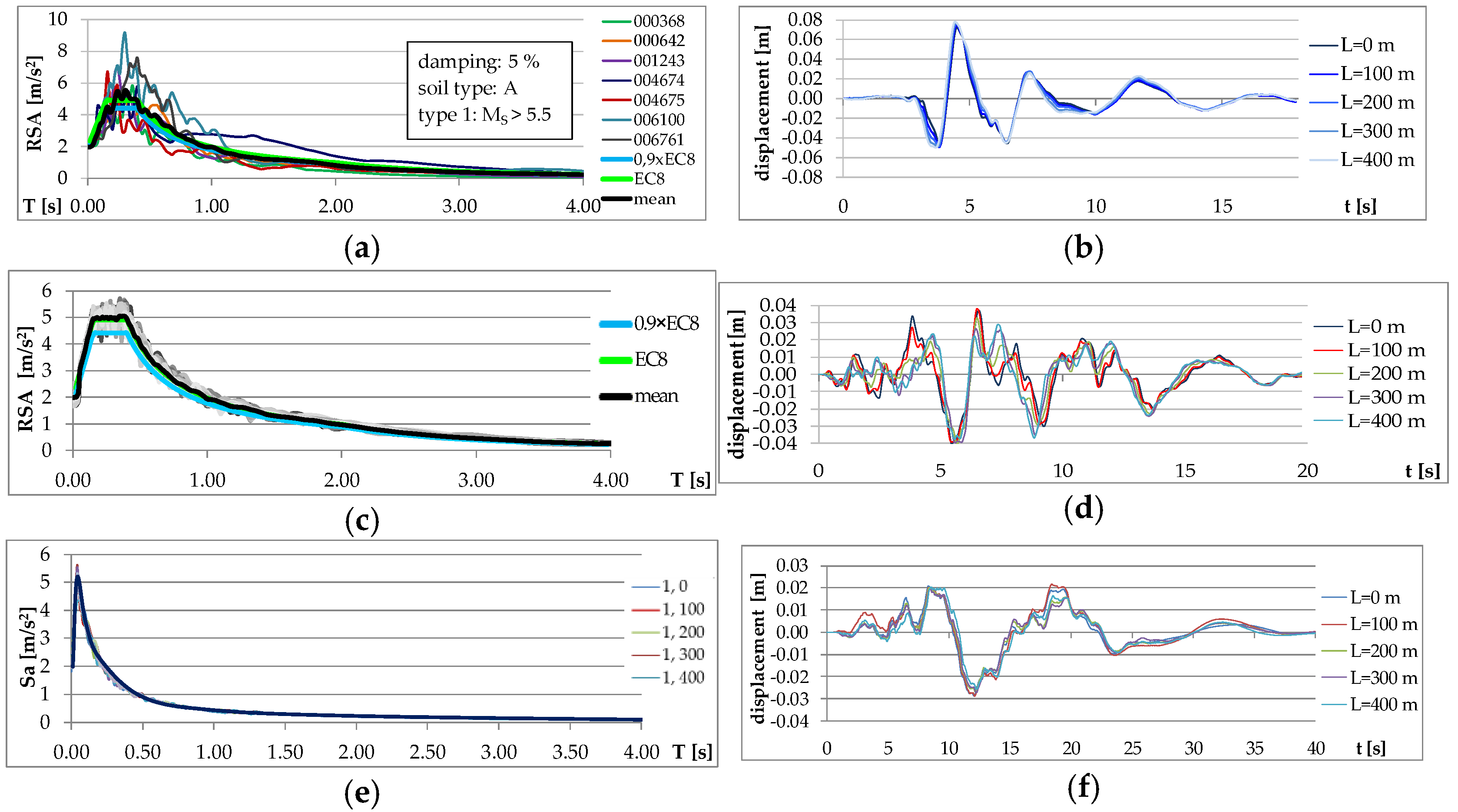
Figure eight. Showtime 2 modes of vibration for bridges: (a) F100; (b) F200; (c) F300; (d) F400.

Figure 8. First ii modes of vibration for bridges: (a) F100; (b) F200; (c) F300; (d) F400.

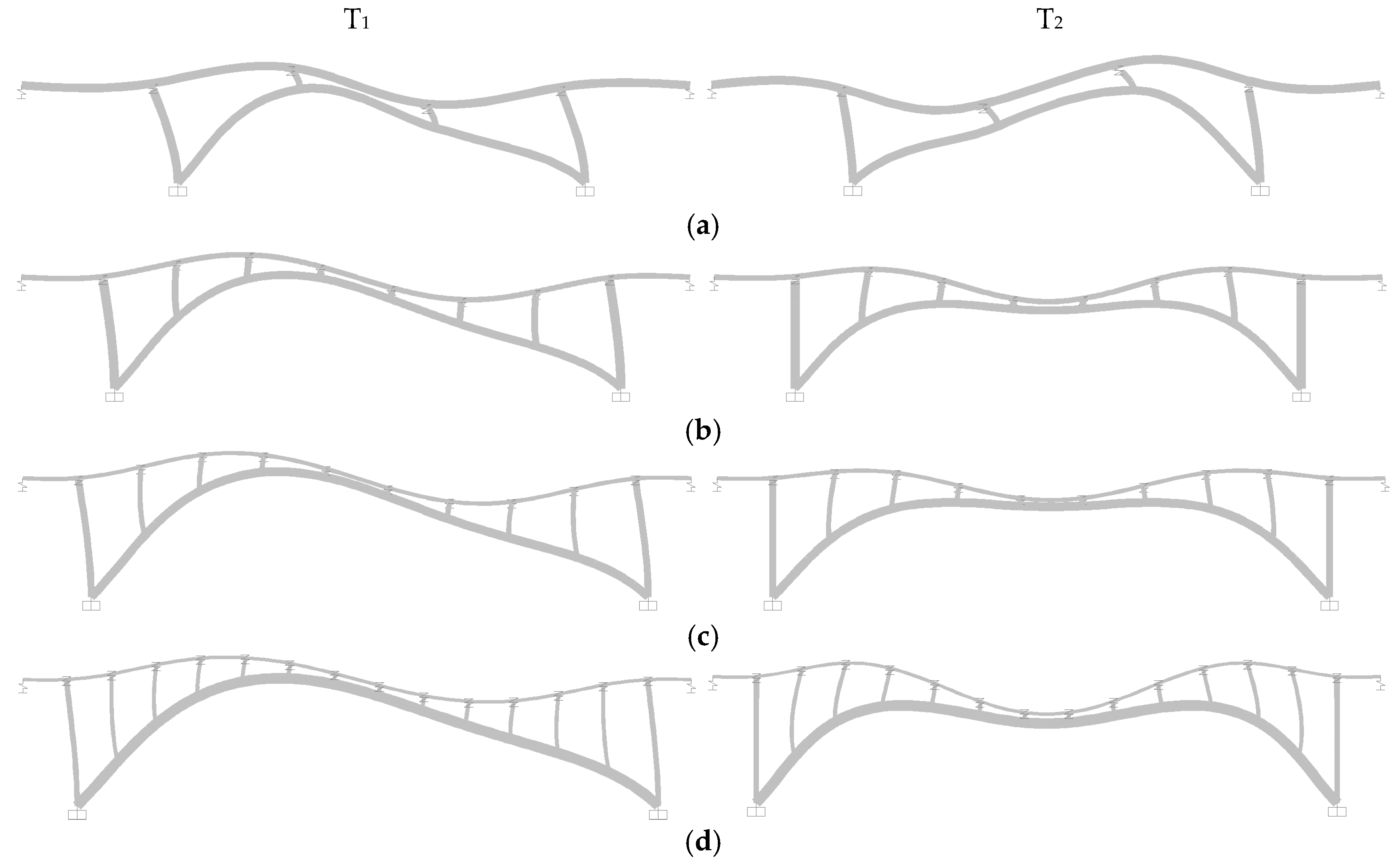
Figure nine. Elastic response spectra EC8 with modal mass participating ratios for all analyzed bridges.

Figure 9. Elastic response spectra EC8 with modal mass participating ratios for all analyzed bridges.

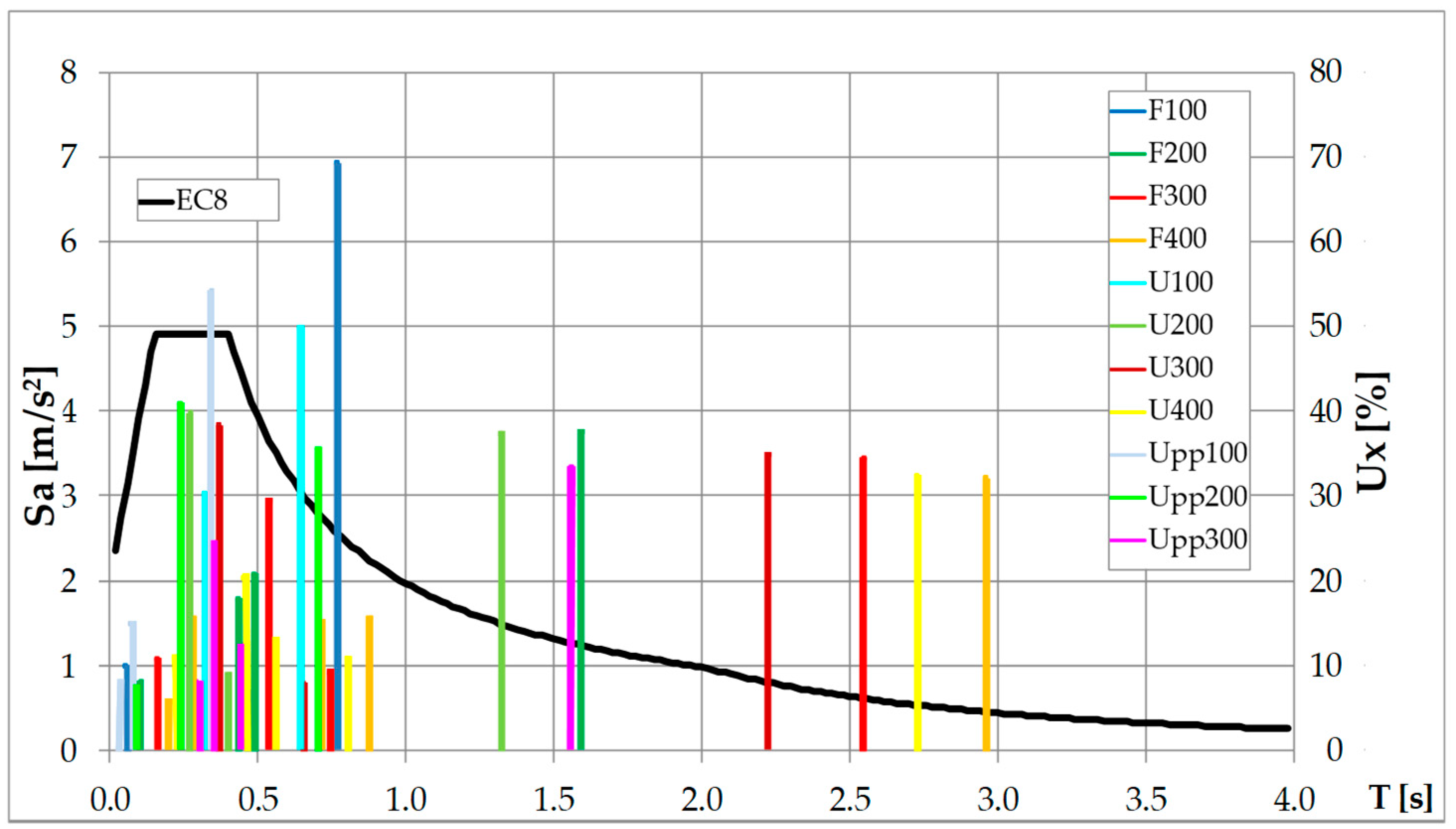
Figure 10. Ratios ρ _one of all analyzed bridges grouped by static arrangement: (a) centric forces; (b) shear forces; (c) bending moments.

Figure 10. Ratios ρ _one of all analyzed bridges grouped by static system: (a) axial forces; (b) shear forces; (c) bending moments.

Effigy eleven. Ratios ρ _ane of all analyzed bridges grouped by static organization: (a) horizontal displacements; (b) vertical displacements.

Figure 11. Ratios ρ ₁ of all analyzed bridges grouped past static organization: (a) horizontal displacements; (b) vertical displacements.

Effigy 12. Ratios ρ _two at arch quarter bridge for: (a) axial forces; (b) bending moments; (c) vertical displacements *. * note: for clarity of the effigy (c), the large ρ ₂ of the bridge Upp100 amounting to 5.4 obtained using the MSRS method was disregarded.

Effigy 12. Ratios ρ ₂ at curvation quarter span for: (a) axial forces; (b) bending moments; (c) vertical displacements *. * note: for clarity of the effigy (c), the big ρ ₂ of the bridge Upp100 amounting to 5.four obtained using the MSRS method was overlooked.

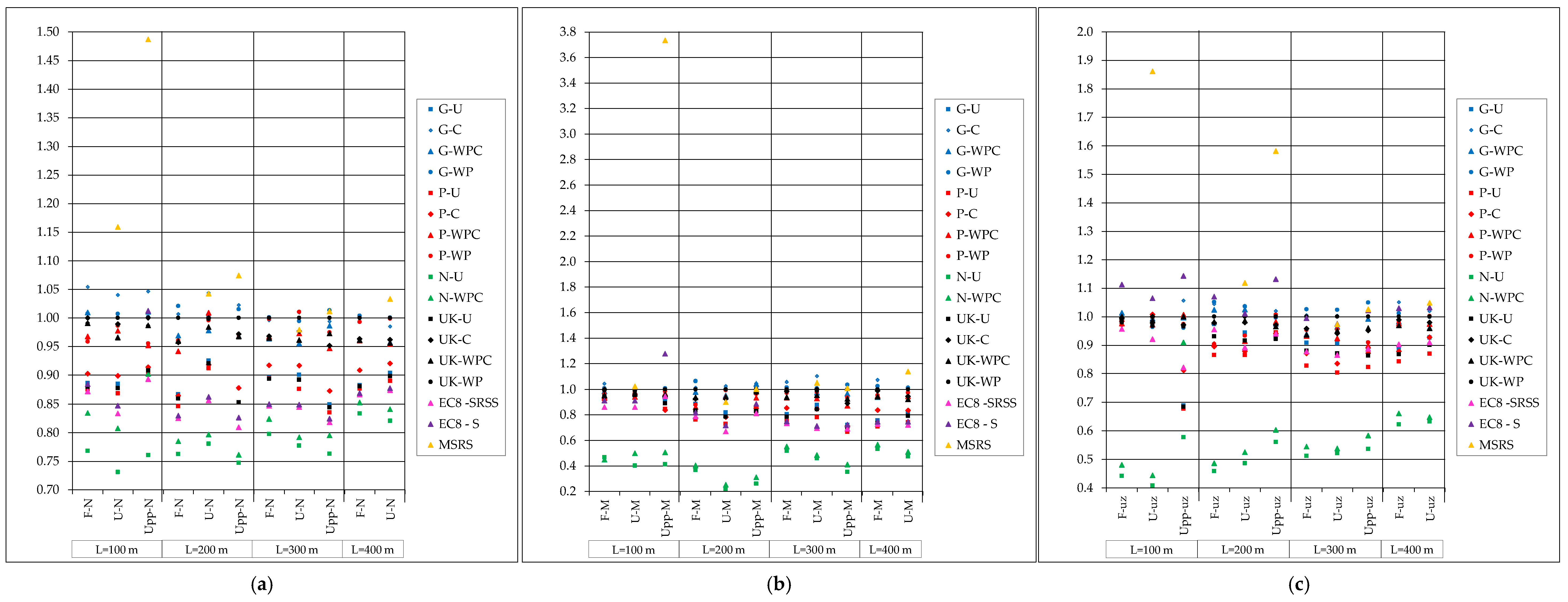
Figure xiii. Ratios ρ _ii at arch crown for: (a) axial forces; (b) angle moments; (c) vertical displacements *. * note: for clarity of the figure (c), the large ρ ₂ of the bridge Upp100 amounting to 3.65 obtained using the MSRS method was disregarded

Figure 13. Ratios ρ _two at arch crown for: (a) centric forces; (b) bending moments; (c) vertical displacements *. * note: for clarity of the figure (c), the large ρ ₂ of the span Upp100 amounting to three.65 obtained using the MSRS method was disregarded

Effigy 14. Pseudo-static (in black colour) and dynamic (in grey colour) function of the response: (a) bridge Upp100; (b) bridge U100; (c) bridge U400.

Effigy xiv. Pseudo-static (in black color) and dynamic (in grey color) part of the response: (a) bridge Upp100; (b) bridge U100; (c) bridge U400.

Tabular array 1. Cross-section dimensions of arches and columns.

Table ane. Cross-department dimensions of arches and columns.

Bridge L [m]	Curvation Outer Dimensions d × h [m]	Arch Outer Web Thickness bt [thou]	Curvation inner Web Thickness ct [chiliad]	Arch Chord Thicknesset [m]	Cavalcade Outer Dimensionsds × bs [k]	Thickness of the Column Chords csouth [one thousand]	Portal Outer Dimensionsdp × bp [m]	Portal Chords Thickness cp [m]
100	10 × 2	0.xxx	0.30	0.45	3.0 × 1.5	0.30	4.0 × 2.0	0.50
200	10 × 3	0.50	0.30	0.50	5.0 × two.5	0.30	6.5 × iii.5	0.50
300	11 × 5	0.fifty	0.50	0.50	v.0 × ii.v	0.thirty	6.5 × 3.v	0.l
400	12 × 7	0.60	0.60	0.60	v.0 × 2.5	0.30	6.5 × three.five	0.l

Table 2. Periods corresponding to kickoff x Ritz vectors of all analyzed bridges [s].

Tabular array 2. Periods corresponding to outset ten Ritz vectors of all analyzed bridges [s].

Ritz v.	Menses [due south]
	F100	U100	Upp100	F200	U200	Upp200	F300	U300	Upp300	F400	U400
1	0.768	0.645	0.344	1.596	1.322	0.705	ii.547	two.226	1.560	2.959	2.726
ii	0.464	0.352	0.255	0.895	0.731	0.443	i.398	1.221	0.880	1.628	ane.497
three	0.424	0.318	0.246	0.485	0.403	0.273	0.746	0.657	0.476	0.878	0.801
4	0.301	0.255	0.215	0.436	0.381	0.239	0.611	0.563	0.453	0.728	0.698
5	0.281	0.224	0.190	0.433	0.275	0.222	0.540	0.419	0.339	0.715	0.550
vi	0.281	0.205	0.189	0.323	0.268	0.219	0.475	0.371	0.321	0.659	0.539
vii	0.254	0.190	0.140	0.282	0.222	0.195	0.387	0.334	0.293	0.613	0.503
8	0.236	0.182	0.123	0.281	0.215	0.171	0.369	0.318	0.291	0.551	0.451
nine	0.177	0.145	0.105	0.260	0.203	0.162	0.355	0.283	0.230	0.444	0.377
10	0.137	0.113	0.079	0.231	0.173	0.161	0.328	0.253	0.223	0.426	0.335

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access commodity distributed under the terms and weather of the Creative Commons Attribution (CC By) license (http://creativecommons.org/licenses/past/4.0/).

We use cookies on our website to ensure you get the best feel.
Read more about our cookies here.

We have simply recently launched a new version of our website.
Help us to further improve by taking role in this short v minute survey here. hither.

baldwinoblas1988.blogspot.com

Source: https://www.mdpi.com/2076-3417/10/1/17/htm